Linear vs. Non-linear: Difference between revisions
No edit summary |
No edit summary |
||
| (One intermediate revision by one other user not shown) | |||
| Line 8: | Line 8: | ||
|} | |} | ||
<!-- Introductory paragraph or topic page summary --> | <!-- Introductory paragraph or topic page summary --> | ||
"Both new and existing structures are constantly being examined to determine if they meet [[stability]] criteria. The traditional procedure is to evaluate [[Sliding Stability|sliding stability]] of these structures using the limit equilibrium method of analysis and to evaluate [[Rotational Stability|rotational stability]] using rigid body assumptions and bearing pressure distributions that vary linearly across the base. Soil and uplift loads on the structure are often based on simplifying assumptions. In the limit equilibrium method, only the stress at failure is considered, usually as represented by the Mohr-Coulomb limit-state criterion. The simplified loads and the Mohr-Coulomb limit-state criterion are then used to obtain a single overall factor of safety against a [[Sliding Stability|sliding stability]] failure. This traditional approach is appropriate for many structures where it is difficult to predict just how a particular failure | "Both new and existing structures are constantly being examined to determine if they meet [[stability]] criteria. The traditional procedure is to evaluate [[Sliding Stability|sliding stability]] of these structures using the limit equilibrium method of analysis and to evaluate [[Rotational Stability|rotational stability]] using rigid body assumptions and bearing pressure distributions that vary linearly across the base. Soil and uplift loads on the structure are often based on simplifying assumptions. In the limit equilibrium method, only the stress at failure is considered, usually as represented by the Mohr-Coulomb limit-state criterion. The simplified loads and the Mohr-Coulomb limit-state criterion are then used to obtain a single overall factor of safety against a [[Sliding Stability|sliding stability]] failure. This traditional approach is appropriate for many structures where it is difficult to predict just how a particular failure mechanism may develop. However, for existing structures where more is known about service state conditions and uplift pressures, it is possible to more precisely predict what stress changes must occur to develop a failure condition. The margin of safety can be more accurately determined when the path to failure, from initial stress conditions to limit state conditions, is known. This path to failure can be investigated using linear elastic and nonlinear finite-element numerical solutions and facture mechanics concepts. Because the deformation of the structure and its foundation is considered in finite element analyses, and because the path to failure can be more realistically characterized through facture mechanics, a more accurate assessment of safety can often be made using advanced analytical methods."<ref name="EM 1110-2-2100">[[Stability Analysis of Concrete Structures (EM 1110-2-2100) | Stability of Concrete Structures (EM 1110-2-2100), USACE, 2005]]</ref> | ||
==Best Practices Resources== | ==Best Practices Resources== | ||
{{Document Icon}} [[Stability Analysis of Concrete Structures (EM 1110-2-2100) | Stability Analysis of Concrete Structures (EM 1110-2-2100), USACE]] | {{Document Icon}} [[Stability Analysis of Concrete Structures (EM 1110-2-2100) | Stability Analysis of Concrete Structures (EM 1110-2-2100), USACE]] | ||
{{Document Icon}} [[Gravity Dam Design (EM 1110-2-2200) | Gravity Dam Design (EM 1110-2-2200), USACE | {{Document Icon}} [[Gravity Dam Design (EM 1110-2-2200) | Gravity Dam Design (EM 1110-2-2200), USACE]] | ||
{{Document Icon}} [[Arch Dam Design (EM 1110-2-2201) | Arch Dam Design (EM 1110-2-2201), USACE | {{Document Icon}} [[Arch Dam Design (EM 1110-2-2201) | Arch Dam Design (EM 1110-2-2201), USACE]] | ||
{{Document Icon}} [[Design of Small Dams | Design of Small Dams, USBR | {{Document Icon}} [[Design of Small Dams | Design of Small Dams, USBR]] | ||
{{Document Icon}} [[Sliding Stability for Concrete Structures (ETL 1110-2-256) | Sliding Stability for Concrete Structures (ETL 1110-2-256), USACE | {{Document Icon}} [[Sliding Stability for Concrete Structures (ETL 1110-2-256) | Sliding Stability for Concrete Structures (ETL 1110-2-256), USACE]] | ||
==Trainings== | ==Trainings== | ||
Latest revision as of 20:51, 11 July 2023
|
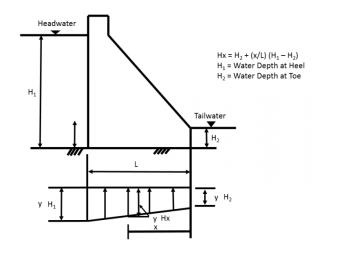
| Learn more about the need to consider uplift pressure when designing a gravity structure at DamFailures.org |
"Both new and existing structures are constantly being examined to determine if they meet stability criteria. The traditional procedure is to evaluate sliding stability of these structures using the limit equilibrium method of analysis and to evaluate rotational stability using rigid body assumptions and bearing pressure distributions that vary linearly across the base. Soil and uplift loads on the structure are often based on simplifying assumptions. In the limit equilibrium method, only the stress at failure is considered, usually as represented by the Mohr-Coulomb limit-state criterion. The simplified loads and the Mohr-Coulomb limit-state criterion are then used to obtain a single overall factor of safety against a sliding stability failure. This traditional approach is appropriate for many structures where it is difficult to predict just how a particular failure mechanism may develop. However, for existing structures where more is known about service state conditions and uplift pressures, it is possible to more precisely predict what stress changes must occur to develop a failure condition. The margin of safety can be more accurately determined when the path to failure, from initial stress conditions to limit state conditions, is known. This path to failure can be investigated using linear elastic and nonlinear finite-element numerical solutions and facture mechanics concepts. Because the deformation of the structure and its foundation is considered in finite element analyses, and because the path to failure can be more realistically characterized through facture mechanics, a more accurate assessment of safety can often be made using advanced analytical methods."[1]
Best Practices Resources
Stability Analysis of Concrete Structures (EM 1110-2-2100), USACE
Gravity Dam Design (EM 1110-2-2200), USACE
Arch Dam Design (EM 1110-2-2201), USACE
Sliding Stability for Concrete Structures (ETL 1110-2-256), USACE
Trainings
On-Demand Webinar: Stability Evaluations of Concrete Dams
On-Demand Webinar: Analysis of Concrete Arch Dams
Citations:
Revision ID: 7164
Revision Date: 07/11/2023